SWS Methodology

Keyboard Command	Feature
`?`	Hide/show help
`shift`+`t`	Hide/show table of contents

URL Command	Feature
`?teacher=[github-user]`	Auto-generated teacher slide

SUA Module Graph

sua-network-graph

SUA Module Invalidation

Re-run Trade Module

sua-network-graph-trade

Re-run Trade and Production Modules

Hold re-run of Food, Stock, Loss and Feed modules until both Trade and Production modules have completed

sua-network-graph-trade-production

Re-run Production and Food Modules

sua-network-graph-production-food

Production Module

Flowchart Production Module

yEd file: 2016-06-20-faoswsProduction.graphml

module-production-yed

Flowchart Livestock Imputation

Public file: livestock_flow.jpg

yEd file: 2016-06-20-faoswsProduction-livestock.graphml

module-production-livestock-yed

Stock Module

Flowchart Stock Module

yEd file: 2016-09-05-faoswsStock.graphml

Report AMIS: 2016-05-18-stocks-amis.pdf

module-stock-yed

Model based on historical changes
URL: file://///HQFILE4/ESS_admin/ESS/Team_working_folder/A/FBS-Methods/OrangeBook/book/6_stocks/Stocks_master.docx
Label: Equations 9, 10

delta stock changes \Delta \mathsf{S}\_{t-i} (&#916S;)
time t
numebr of previous stock changes k
error term \epsilon_(t) (ε)

\[ \Delta \mathsf{S}_{t} = \beta \left( \sum\limits_{i=1}^{k} \Delta \mathsf{S}_{t-i} \right) + \epsilon_{t}\ \]

We could alternatively express this as

\[ \Delta \mathsf{S}_{t} \sim N \left( \beta \sum\limits_{i=1}^{k} \Delta \mathsf{S}_{t-i} , \sigma^{2} \right) \]

R `lm` Implementation

The current implementation of the module is different from the Orange Book. The module is using only delta production. The formula currently included in the Orange Book may need to be subject to revision.

  stocksModel <- lm(deltaStocks ~ deltaProduction, 
          data = newSuaData[deltaProduction != 0 & 
                              deltaStocks != 0])

Tourist Module

Flowchart tourist Module

URL: Tourist Flowchart.html

module-tourist-drawio

Model based on historical changes

URL: file://///HQFILE4/ESS_admin/ESS/Team_working_folder/A/FBS-Methods/OrangeBook/book/9_Tourists/Tourist%20Consumption_master.docx
Label: Equations 23, 24, 25

Calculate total number of tourist days N\_{T}

\[ N_{T} = N_{D} + N_{O} \bar{D} \]

number of day visitors N\_{D}
number of overnight visitors N\_{O}
information on the average number of nights stayed within each country \bar{D}

Change in amount of food availability for commodity i in country j

\[ \Delta TC_{ij} = - \sum_{k = 1, k \ne j}^{m} N_{jk} f_{ij} + \sum_{l = 1, l \ne j}^{m} N_{lj} f_{il} \]

Suggested alternative notation:

\[ Net TC_{ij} = \sum_{l = 1, l \ne j}^{m} N_{lj} f_{il} - \left( \sum_{k = 1, k \ne j}^{m} N_{jk} \right) * f_{ij} \]

$N_{lj}$ represents the number of tourists travelling from country $l$ to country $j$
$f_{il}$ represents the historic amount of daily nutritients consumed within commodity $i$ and in country $l$
$k$ represents any third country
$m$ represents the set of possible countries in which tourism can occur

This can be simplified to

\[ \Delta TC_{ij} = - N_{T} f_{ij} + \sum_{l = 1, l \ne j}^{m} N_{lj} f_{il} \]

R module Implementation

The current implementation of the module is different from the Orange Book. […]

  touristModel <- lm(...)

Food Module

Compact Flowchart Food Module

module-food-compact-yed

Flowchart Food Module

module-food-yed

Log-log function

country $i$
commodity $j$
trendfactor $\phi_{i}$
income elasticity of demand $\epsilon_{ij}$

Per-capita Food Consumption:

\[ \mathsf{FoodPC}_{t,ij} = \mathsf{FoodPC}_{t-1,ij} + e^{\epsilon_{ij} \log \left( \Delta \mathsf{Y}_{t,i} \right) } + \phi_{i} * \mathsf{FoodPC}_{t-1,ij} \]

This corresponds to

\[ \mathsf{FoodPC}_{t,ij} = \left( 1 + \phi_{i} \right) \mathsf{FoodPC}_{t,ij} + e^{\epsilon_{ij} \log \left( \Delta \mathsf{Y}_{t,i} \right) } \]

expanding per-capita food consumption

\[ \mathsf{FoodPC}_{t,ij} = \frac{ \mathsf{Food}_{t,ij} }{ \mathsf{Pop}_{t,i} } \]

\[ \frac{ \mathsf{Food}_{t,ij} }{ \mathsf{Pop}_{t,i} } = \left( 1 + \phi_{i} \right) \frac{ \mathsf{Food}_{t-1,ij} }{ \mathsf{Pop}_{t-1,i} } + e^{\epsilon_{ij} \log \left( \Delta \mathsf{Y}_{t,i} \right) } \]

multiply both sides with $Pop_{t, ij}$

\[ \mathsf{Food}_{t,ij} = \mathsf{Pop}_{t,i} * \left[ \left( 1 + \phi_{i} \right) \frac{ \mathsf{Food}_{t-1,ij} }{ \mathsf{Pop}_{t-1,i} } + e^{\epsilon_{ij} \log \left( \Delta \mathsf{Y}_{t,i} \right) } \right] \]

\[ \mathsf{Food}_{t,ij} = \frac{ \mathsf{Pop}_{t,i} }{ \mathsf{Pop}_{t-1,i} } * \left( 1 + \phi_{i} \right) \mathsf{Food}_{t-1,ij} + \mathsf{Pop}_{t,i} * e^{\epsilon_{ij} \log \left( \Delta \mathsf{Y}_{t,i} \right) } \]

with

\[ \Delta \mathsf{Pop}_{t,i} = \frac{ \mathsf{Pop}_{t,i} }{ \mathsf{Pop}_{t-1,i} } \]

it becomes

\[ \mathsf{Food}_{t,ij} = \Delta \mathsf{Pop}_{t,i} * \left( 1 + \phi_{i} \right) \mathsf{Food}_{t-1,ij} + \mathsf{Pop}_{t,i} * e^{\epsilon_{ij} \log \left( \Delta \mathsf{Y}_{t,i} \right) } \]

where $\Delta Y_{t,i}$ is the per-capita GDP change

\[ \Delta \mathsf{Y}_{t,i} = \frac{ \mathsf{GDPPC}_{t,i} }{ \mathsf{GDPPC}_{t-1,i} } \]

###Linear function

Per-capita Food Consumption: \[ \mathsf{FoodPC}_{t,ij} = \mathsf{FoodPC}_{t-1,ij} + \phi_{i} * \mathsf{FoodPC}_{t-1,ij} \]

This corresponds to

\[ \frac{ \mathsf{Food}_{t,ij} }{ \mathsf{Pop}_{t,i} } = \left( 1 + \phi_{i} \right) \frac{ \mathsf{Food}_{t-1,ij} }{ \mathsf{Pop}_{t-1,i} } \]

multiply both sides with $Pop_{t, ij}$

\[ \mathsf{Food}_{t,ij} = \mathsf{Pop}_{t,i} * \left[ \left( 1 + \phi_{i} \right) \frac{ \mathsf{Food}_{t-1,ij} }{ \mathsf{Pop}_{t-1,i} } \right] \]

\[ \mathsf{Food}_{t,ij} = \frac{ \mathsf{Pop}_{t,i} }{ \mathsf{Pop}_{t-1,i} } * \left( 1 + \phi_{i} \right) { \mathsf{Food}_{t-1,ij} } \]

\[ \mathsf{Food}_{t,ij} = \Delta \mathsf{Pop}_{t,i} * \left( 1 + \phi_{i} \right) \mathsf{Food}_{t-1,ij} \]

Semi-log function

Per-capita Food Consumption:

\[ \mathsf{FoodPC}_{t,ij} = \mathsf{FoodPC}_{t-1,ij} * \left[1 + \epsilon_{ij} \log \left( \Delta \mathsf{Y}_{t,i} \right) \right]+ \phi_{i} * \mathsf{FoodPC}_{t-1,ij} \]

\[ \mathsf{FoodPC}_{t,ij} = \mathsf{FoodPC}_{t-1,ij} * \left[1 + \epsilon_{ij} \log \left( \Delta \mathsf{Y}_{t,i} \right) + \phi_{i} \right] \]

\[ \frac{ \mathsf{Food}_{t,ij} }{ \mathsf{Pop}_{t,i} } = \frac{ \mathsf{Food}_{t-1,ij} }{ \mathsf{Pop}_{t-1,i} } * \left[1 + \epsilon_{ij} \log \left( \Delta \mathsf{Y}_{t,i}\right) + \phi_{i} \right] \]

multiply both sides with $Pop_{t, ij}$

\[\mathsf{Food}_{t,ij} = \frac{ \mathsf{Pop}_{t,i} }{ \mathsf{Pop}_{t-1,i} } * \mathsf{Food}_{t-1,ij} * \left[1 + \epsilon_{ij} \log \left( \Delta \mathsf{Y}_{t,i} \right) + \phi_{i}\right] \]

\[ \mathsf{Food}_{t,ij} = \Delta \mathsf{Pop}_{t,i} * \mathsf{Food}_{t-1,ij} * \left[1 + \epsilon_{ij} \log \left( \Delta \mathsf{Y}_{t,i}\right) + \phi_{i}\right] \]

Log-inverse function

Per-capita Food Consumption:

\[ \mathsf{FoodPC}_{t,ij} = \mathsf{FoodPC}_{t-1,ij} * e^{\epsilon_{ij} \left( 1 - \frac{ \mathsf{1}}{ \Delta \mathsf{Y}_{t,i} } \right)} + \phi_{i} * \mathsf{FoodPC}_{t-1,ij} \]

\[ \mathsf{FoodPC}_{t,ij} = \mathsf{FoodPC}_{t-1,ij} * \left[ e^{\epsilon_{ij} \left( 1 - \frac{ \mathsf{1}}{ \Delta \mathsf{Y}_{t,i} } \right)} + \phi_{i}\right] \]

\[ \frac{ \mathsf{Food}_{t,ij} }{ \mathsf{Pop}_{t,i} } = \frac{ \mathsf{Food}_{t-1,ij} }{ \mathsf{Pop}_{t-1,i} } * \left[ e^{\epsilon_{ij} \left( 1 - \frac{ \mathsf{1}}{ \Delta \mathsf{Y}_{t,i} } \right)} + \phi_{i}\right] \]

multiply both sides with $Pop_{t, ij}$

\[\mathsf{Food}_{t,ij} = \frac{ \mathsf{Pop}_{t,i} }{ \mathsf{Pop}_{t-1,i} } * \mathsf{Food}_{t-1,ij} * \left[ e^{\epsilon_{ij} \left( 1 - \frac{ \mathsf{1}}{ \Delta \mathsf{Y}_{t,i} } \right)} + \phi_{i} \right] \]

\[ \mathsf{Food}_{t,ij} = \Delta \mathsf{Pop}_{t,i} * \mathsf{Food}_{t-1,ij} * \left[ e^{\epsilon_{ij} \left( 1 - \frac{ \mathsf{1}}{ \Delta \mathsf{Y}_{t,i} } \right)} + \phi_{i} \right] \]

Industrial Use Module

Flowchart Industrial Use Module

module-industrial-use-yed

Feed Module

Loss Module

Flowchart Loss Module

Hierarchical linear model (HLM)

URL: file://///HQFILE4/ESS_admin/ESS/Team_working_folder/A/FBS-Methods/OrangeBook/book/11_loss/Loss_master.docx
Label: Equation 27a-e

\[ \log \left( \mathsf{Loss}_{ijklm} \right) = \alpha_{1} t + \alpha_{2ijkl} \log \left( \mathsf{Production}_{ijklm} + 1 \right) + \mathsf{A}_{ijklm} \]

\[ \alpha_{2ijkl} = \beta_{20} + \beta_{2ijk} \left( \mathsf{Country:Commodity} \right)_{ijkl} + \mathsf{B}_{ijkl} \]

\[ \beta_{2ijk} = \gamma_{20} + \gamma_{2ij} \left( \mathsf{Commodity} \right) + \mathsf{C}_ijk \]

\[ \gamma_{2ij} = \delta_{20} + \delta_{2i} \left( \mathsf{Food Group} \right) + D_{ij} \]

\[ \delta_{2i} = \zeta_{20} + \zeta_{21} \left( \mathsf{Food Perishable Group}_{i} \right) + \mathsf{E}_{i} \]

R `lme4` Implementation

The current implementation of the module is different from the Orange Book. The module includes imports (measuredElementTrade_5610). The formula currently included in the Orange Book may need to be subject to revision.

  lossLmeModel =
    lmer(log(Value_measuredElement_5016 + 1) ~
           -1 +
           timePointYears +
           log(Value_measuredElement_5510 + 1) + 
           (-1 + log(Value_measuredElement_5510 + 1)|
            foodPerishableGroup/foodGroupName/measuredItemCPC/geographicAreaM49)+
           log(Value_measuredElementTrade_5610 + 1) +
           (-1 + log(Value_measuredElementTrade_5610 + 1)|
            measuredItemCPC/geographicAreaM49),
         data = finalModelData)

network-repository

monitor suggested changes (e.g. foodPerishableGroup.csv)
use as development environment
consider for integration with repository used by SWS

Configuration

git remote add upstream https://github.com/SWS-Methodology/faoswsLoss.git
git remote set-url origin file://t:/Team_working_folder/A/FBS-Modules/faoswsLoss/.git

Seed Module

Trade Module

Outlier Detection in “Complete Trade Flow” Module

currently, only the data for 2011 is considered
the result has been created using the validate package
values are categorized as outliers according to their unit value uv = value / qty
on the y-axis, the ratio of observations categorized as “outliers” is shown
for example if the “outlier coefficient” is set to the value 1.5 (x-axis), this results in 6.4% of the observations to be considered as “outliers” (y-axis)
the variable qty is a combined result of weight (mass) and supplementary quantity measures and represents an item measured in metric tons
for values that are considered as outliers, the weight is calculated as qty = value / uv where uv represents the median unit value for each reporter
observations where the weight is re-calculated receive the flagObservationStatus = I and flagMethod = e

Sensitivity of outlier to coefficient

coef argument of boxplot.stats R function in grDevices: determines how far the plot ‘whiskers’ extend out from the box. If coef is positive, the whiskers extend to the most extreme data point which is no more than coef times the length of the box away from the box. A value of zero causes the whiskers to extend to the data extremes (and no outliers be returned). The default value for coef is 1.5. The interquartile range IQR corresponds to the length of the box, i.e. the difference between Q1 and Q3.

Source: https://en.wikipedia.org/wiki/Box_plot#/media/File:Boxplot_vs_PDF.svg

faoswsTrade/modules/complete_tf_cpc/main.R

# Outlier detection

tradedata <- tradedata %>%
  group_by_(~year, ~reporter, ~flow, ~hs) %>%
  mutate_(
    uv_reporter = ~median(uv, na.rm = T),
    outlier = ~uv %in% boxplot.stats(uv, coef = out_coef, do.conf = F)$out) %>%
  ungroup()

Adjustment Notes applied to Comtrade

Example rows from the adjustments SWS datatable

year	flow	hs	fcl	partner	weight	qty	value	special	reporter
2012	1	NA	17	NA	10	NA	NA	NA	8
2005	2	NA	1168	NA	100	NA	NA	NA	11
NA	NA	NA	836	NA	0.6	NA	NA	NA	52
2013	4	NA	702	194	0.1	NA	NA	NA	13
2011	1	NA	1061	NA	0.1	NA	NA	NA	37
2013	2	9030000	671	231	10	NA	NA	NA	33

The table below shows combinations of flow, hs, partner and reporter dimensions with n >= 10 occurences. For each of these combinations, the relevant rows have been extracted from the adjustments table and sorted by year in ascending order.

rowname	flow	hs	partner	reporter	count
1	1	4041048	67	210	13
2	2	8051000	114	215	11
3	1	15220099	68	150	10
4	2	22019000	106	198	10

[[1]]

year	flow	hs	fcl	partner	weight	qty	value	special	reporter
1999	1	4041048	NA	67	0.01	NA	NA	NA	210
2001	1	4041048	890	67	0.01	NA	NA	NA	210
2002	1	4041048	890	67	0.01	NA	NA	NA	210
2003	1	4041048	890	67	0.01	NA	NA	NA	210
2004	1	4041048	890	67	0.01	NA	NA	NA	210
2006	1	4041048	890	67	0.01	NA	NA	NA	210
2007	1	4041048	890	67	0.01	NA	NA	NA	210
2008	1	4041048	890	67	0.01	NA	NA	NA	210
2009	1	4041048	890	67	0.01	NA	NA	NA	210
2010	1	4041048	890	67	0.01	NA	NA	NA	210
2011	1	4041048	890	67	0.01	NA	NA	NA	210
2012	1	4041048	890	67	0.01	NA	NA	NA	210
2013	1	4041048	890	67	0.01	NA	NA	NA	210

[[2]]

year	flow	hs	fcl	partner	weight	qty	value	special	reporter
1997	2	8051000	490	114	0.1	NA	NA	NA	215
2000	2	8051000	490	114	0.1	NA	NA	NA	215
2001	2	8051000	490	114	0.1	NA	NA	NA	215
2002	2	8051000	490	114	0.1	NA	NA	NA	215
2003	2	8051000	490	114	0.1	NA	NA	NA	215
2004	2	8051000	490	114	0.1	NA	NA	NA	215
2005	2	8051000	490	114	0.1	NA	NA	NA	215
2006	2	8051000	490	114	0.1	NA	NA	NA	215
2007	2	8051000	490	114	0.1	NA	NA	NA	215
2009	2	8051000	490	114	0.1	NA	NA	NA	215
2012	2	8051000	490	114	10	NA	NA	NA	215

[[3]]

year	flow	hs	fcl	partner	weight	qty	value	special	reporter
1999	1	15220099	NA	68	0.1	NA	NA	NA	150
2000	1	15220099	1277	68	0.1	NA	NA	NA	150
2007	1	15220099	1277	68	NA	NA	weight	NA	150
2008	1	15220099	1277	68	NA	NA	weight	NA	150
2009	1	15220099	1277	68	NA	NA	m570	NA	150
2010	1	15220099	1277	68	0.01	NA	NA	NA	150
2010	1	15220099	1277	68	NA	NA	weight	NA	150
2011	1	15220099	NA	68	f0	NA	NA	NA	150
2012	1	15220099	1277	68	NA	NA	weight	NA	150
2013	1	15220099	1277	68	NA	NA	m1000	NA	150

[[4]]

year	flow	hs	fcl	partner	weight	qty	value	special	reporter
2004	2	22019000	631	106	0.01	NA	NA	NA	198
2005	2	22019000	631	106	0.001	NA	NA	NA	198
2006	2	22019000	631	106	0.01	NA	NA	NA	198
2007	2	22019000	631	106	0.001	NA	NA	NA	198
2008	2	22019000	631	106	0.01	NA	NA	NA	198
2009	2	22019000	631	106	0.001	NA	NA	NA	198
2010	2	22019000	631	106	0.001	NA	NA	NA	198
2011	2	22019000	631	106	0.01	NA	NA	NA	198
2012	2	22019000	631	106	0.001	NA	NA	NA	198
2013	2	22019000	631	106	0.01	NA	NA	NA	198

Characters preceeding numeric weights and character weights

## [1] "f"      "m"      "o"      "qty"    "value"  "weight"

Distribution of numeric weights

## smaller than one
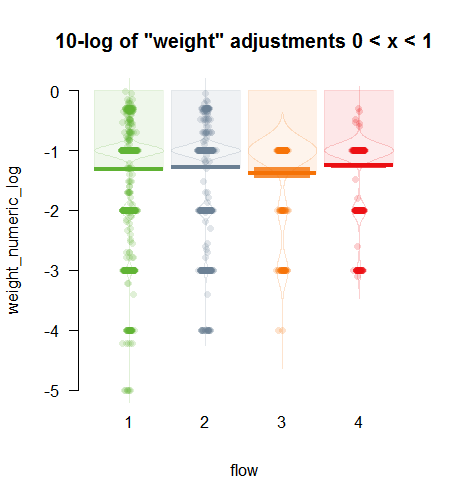
adjustments_list[["weight"]][["numeric"]] %>% .[. < 1] %>% base::summary()

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##  0.0000  0.0100  0.1000  0.2082  0.3667  0.9800

## larger than or equal to one
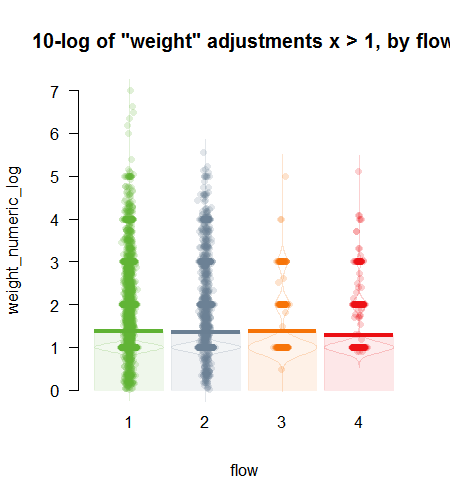
adjustments_list[["weight"]][["numeric"]] %>% .[. >= 1] %>% base::summary()

##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
##        1       16       91    19440      711 10000000

Visual display of numeric weight distribution by type of trade flow. Log values are shown for better display.

report-adjustments-csv-pirateplot-1

Based on the filter in the module, two files have been prepared

adjustments = adjustments %>%
  filter_(~!(is.na(year) &
               weight == 1000))

1726 observations where weight is equal to 1000: adjustments_weigth1000.csv
1599 observations where weight is equal to 1000 and year is specified: adjustments_weigth1000_year.csv

I.e. there are only 127 out of the 1726 observations where no year is specified. This corresponds to 7.3 % of the observations.

Flowchart Trade Module

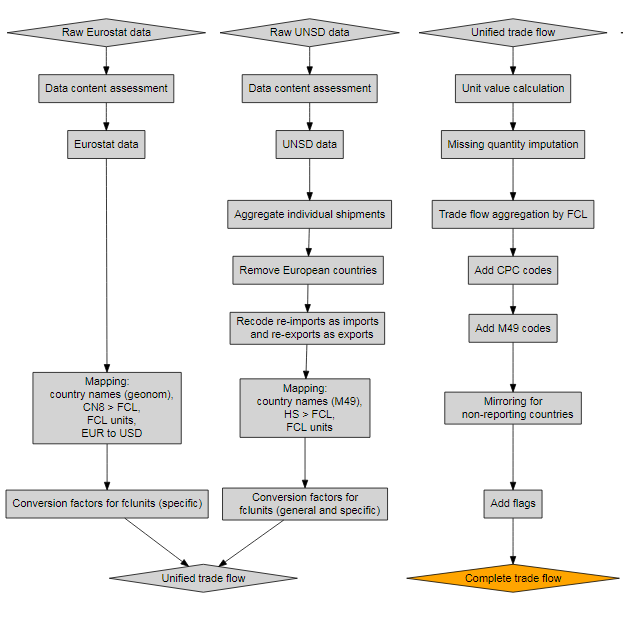
Raw Data Transformation

SWS-Methodology/faoswsTrade/vignettes/Documentation/assets/trade_1.png

module-trade-github-trade_1

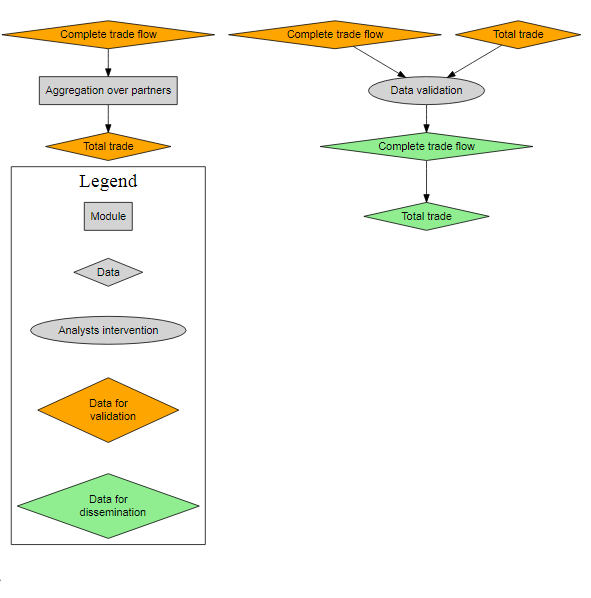
Imputation and Aggregation

SWS-Methodology/faoswsTrade/vignettes/Documentation/assets/trade_2.png

module-trade-github-trade_2

Standardization Module

Flowchart Standardization Module

module-standardization-yed

Imputation Module

Balancing Module

Flag Module

Util Module

Modules Module

GitHub Issues by Repository

faoswsFeed

faoswsFood

faoswsIndustrial

faoswsLoss

faoswsProduction

faoswsSeed

faoswsStandardization

Add intermediate save to balanceResidual

When module compiles unbalanced SUA, it should create an element which is the availability in the crude balancing step. This can be done as a SaveData call in balanceResidual. Probably to the sua table?

Incomplete extraction rates and shares

I’m fairly sure that these tables are incomplete. They come from the aupus_ratio table - I need to check their status.

Nutritive factors seem missing

We currently have no calorie/protein/fat factors for wheat flour (across all countries and all years). Clearly we must be missing some data…

Specify food/feed/industrial/… commodities

In the standardization process, the balanceResidual function will balance the SUA level commodities by assigning imbalances to a specific variable. For example, if the balance for flour has an excess of 5,000 tons, this amount will be added to the food of flour (while for bran it would be allocated to feed). We need to implement the list specifying what variable certain commodities get allocated to (food, feed, industrial uses, etc.) and incorporate this information into the balanceResidual function.

faoswsStock

faoswsTourist

faoswsTrade

EU Commission - Combined Nomenclature table for 1999-2008

Currently, the Datatables don’t seem to be on the working system.

Key not found for dimension measuredItemCPC

There are a number of CPC codes that aren’t in the destination table for Total trade. I’m not sure as to why that is, but among them are 01241.90, 01919.96 and 21419.91.

Issues PDF by Repository

The following links can be accessed after logging in to hostedredmine.com: user: faoessatest
login: 5udSPY57

Food food-module/issues.pdf
Stocks stocks-module/issues.pdf
Tourist tourist-module/issues.pdf
Industrial Use industrial-use/issues.pdf

Sub-Modules by Package

Each of the subfolders in /modules is supposed to contain a main.R and a metadata.xml file

 faoswsFeed
:   impute_feed

faoswsFood
:   food_input_validation  
    impute_food

faoswsIndustrial
:   impute_industrial

faoswsLoss
:   impute_loss  
    loss_input_validation

faoswsProduction
:   balance_production_identity  
    impute_livestock  
    impute_non_livestock  
    production_input_validation  
    status_report

faoswsSeed
:   seed_imputation  
    seed_input_validation

faoswsStandardization
:   pullDataToSUA  
    standardization

faoswsStock
:   impute_stocks

faoswsTourist
:   impute_tourist

faoswsTrade
:   complete_tf_cpc  
    total_trade_CPC

R Scripts by Package

 faoswsFeed
:   animalFunctions.R  
    ass_energy_factor.r  
    ass_protein_factor.r  
    buffalo_energy_factor.r  
    buffalo_protein_factor.r  
    calculateAnimalUnits.R  
    calculateAquaDemand.r  
    calculateFeedDemand.R  
    calculateIR.R  
    calculateLivestockDensity.R  
    camel_energy_factor.r  
    camel_protein_factor.r  
    cattle_energy_factor.r  
    cattle_protein_factor.r  
    chicken_energy_factor.r  
    chicken_protein_factor.r  
    data.R  
    duck_energy_factor.r  
    duck_protein_factor.r  
    faoswsFeed-package.R  
    feedAvail.R  
    getAnimalStocks.R  
    getQueryKey.R  
    goat_energy_factor.r  
    goat_protein_factor.r  
    goose_energy_factor.r  
    goose_protein_factor.r  
    horse_energy_factor.r  
    horse_protein_factor.r  
    mule_energy_factor.r  
    mule_protein_factor.r  
    optimizeFeed.R  
    pig_energy_factor.r  
    pig_protein_factor.r  
    rabbit_energy_factor.r  
    rabbit_protein_factor.r  
    sheep_energy_factor.r  
    sheep_protein_factor.r  
    turkey_energy_factor.r  
    turkey_protein_factor.r

faoswsFood
:   calculateFood.R  
    commodity2FunctionalForm.R  
    FoodModule.R  
    functionalForms.R  
    getCommodityClassification.R  
    getFoodData.R

faoswsIndustrial
:   

faoswsLoss
:   addHeadingsFCL.R  
    faoswsLoss-package.R  
    getImportData.R  
    getLossData.R  
    getLossFoodGroup.R  
    getProductionData.R  
    getSelectedLossData.R  
    imputeLoss.R  
    mergeAllLossData.R  
    removeCarryLoss.R  
    requiredItems.R  
    saveImputedLoss.R

faoswsProduction
:   balanceAreaHarvested.R  
    balanceProduction.R  
    balanceProductionTriplet.R  
    computeYield.R  
    ensureProductionInputs.R  
    ensureProductionOutputs.R  
    expandMeatSessionSelection.R  
    faoswsProduction-package.R  
    getAllHistory.R  
    getAllYieldKey.R  
    getAnimalMeatMapping.R  
    getImputationParameters.R  
    getProductionData.R  
    getProductionFormula.R  
    getYieldData.R  
    imputeProductionTriplet.R  
    isPrimary.R  
    nonImputationItems.R  
    okrapd.R  
    processProductionDomain.R  
    productionFormulaParameters.R  
    productionProcessingParameters.R  
    selectImputationItem.R  
    selectMeatCodes.R  
    transferParentToChild.R

faoswsSeed
:   areaRemoveZeroConflict.R  
    buildCPCHierarchy.R  
    ensureNoConflictingAreaSownHarvested.R  
    faoswsSeed-package.R  
    fillCountrySpecificSeedRate.R  
    fillGeneralSeedRate.R  
    getAllAreaData.R  
    getAllCountries.R  
    getAllItemCPC.R  
    getAllYears.R  
    getAreaData.R  
    getCountryGeneralSeedRate.R  
    getCountrySpecificSeedRate.R  
    getOfficialSeedData.R  
    getSelectedSeedData.R  
    getWorldBankClimateData.R  
    imputeAreaSown.R  
    mergeAllSeedData.R  
    removeCarryForward.R  
    removeManualEstimation.R  
    saveSeedData.R  
    seedData.R

faoswsStandardization
:   addMissingElements.R  
    adjustCommodityTree.R  
    balanceResidual.R  
    calculateAvailability.R  
    collapseEdges.R  
    computeFbsAggregate.R  
    defaultStandardizationParameters.R  
    elementCodesToNames.R  
    elementNamesToCodes.R  
    faoswsStandardization-package.R  
    fbsTree.R  
    finalStandardizationToPrimary.R  
    findProcessingLevel.R  
    getFBSTree.R  
    getOldCommodityTree.R  
    mapCommodityTree.R  
    markUpdated.R  
    plotCommodityTrees.R  
    plotSingleTree.R  
    printSUATable.R  
    processForward.R  
    standardizationWrapper.R  
    standardizeTree.R  
    usaWheat.R

faoswsStock
:   getAllCountries.R  
    getProductionData.R  
    getStockData.R  
    getStocksCPC.R  
    getTotalTradeData.R

faoswsTourist
:   getAllCountries.R  
    getAllItemCPC.R  
    getCommodityClassification.R  
    getFoodConsumption.R  
    getNutrientConversionFactor.R

faoswsTrade
:   applyadj.R  
    convertComtradeM49ToFAO.R  
    convertGeonom2FAO.R  
    convertHS2FCL.R  
    convertMeasuredElementTrade.R  
    convertTLPartnerToFAO.R  
    data.R  
    descFCL.R  
    faoAreaName.R  
    getAgriHSCodes.R  
    getAllItems.R  
    getlistofadjs.R  
    hsInRange.R  
    is.SWSEnvir.R  
    trailingDigits.R  
    trailingDigits2.R  
    verifyTarifflinePartners.R

SUA Module Graph

SUA Module Invalidation

Re-run Trade Module

Re-run Trade and Production Modules

Re-run Production and Food Modules

Production Module

Flowchart Production Module

Flowchart Livestock Imputation

Stock Module

Flowchart Stock Module

R lm Implementation

Tourist Module

Flowchart tourist Module

R module Implementation

Food Module

Compact Flowchart Food Module

Flowchart Food Module

Log-log function

Semi-log function

Log-inverse function

Industrial Use Module

Flowchart Industrial Use Module

Feed Module

Loss Module

Flowchart Loss Module

Hierarchical linear model (HLM)

R lme4 Implementation

git repository on network share

Configuration

Seed Module

Trade Module

Outlier Detection in “Complete Trade Flow” Module

Sensitivity of outlier to coefficient

Adjustment Notes applied to Comtrade

Flowchart Trade Module

Raw Data Transformation

Imputation and Aggregation

Standardization Module

Flowchart Standardization Module

Imputation Module

Balancing Module

Flag Module

Util Module

Modules Module

GitHub Issues by Repository

faoswsFeed

faoswsFood

faoswsIndustrial

faoswsLoss

faoswsProduction

faoswsSeed

faoswsStandardization

faoswsStock

faoswsTourist

faoswsTrade

Issues PDF by Repository

Sub-Modules by Package

R Scripts by Package

Table of Contents

R `lm` Implementation

R `lme4` Implementation